えが簡単な分数（５/１６）になることに、数学の神秘を感じます。この問題は、平成２４年度
の中央大学理工学部で出題されました。
実際に解いてみたいと思います。
与式＝ｓｉｎ（π/５）ｓｉｎ（２π/５）ｓｉｎ（２π/５）ｓｉｎ（π/５）
＝ｓｉｎ2（π/５）ｓｉｎ2（２π/５）
＝（１/４）（１−ｃｏｓ（２π/５））（１−ｃｏｓ（４π/５））
＝（１/４）（１−（ｃｏｓ（２π/５）＋ｃｏｓ（４π/５））＋ｃｏｓ（２π/５）ｃｏｓ（４π/５））
＝（１/４）（１−２ｃｏｓ（３π/５）ｃｏｓ（π/５））＋ｃｏｓ（３π/５）ｃｏｓ（π/５））
＝（１/４）（１−ｃｏｓ（３π/５）ｃｏｓ（π/５））
ここで、 π/５＝θ とおくと、 ５θ＝π より、 ３θ＝π−２θ
ｃｏｓ３θ＝ｃｏｓ（π−２θ）＝−ｃｏｓ２θ なので、
−ｃｏｓ（３π/５）ｃｏｓ（π/５）＝ｃｏｓ（π/５）ｃｏｓ（２π/５）
よって、 与式＝（１/４）（１＋ｃｏｓ（π/５）ｃｏｓ（２π/５））
また、 ｓｉｎ３θ＝ｓｉｎ（π−２θ）＝ｓｉｎ２θ より、 ３ｓｉｎθ−４ｓｉｎ3θ＝２ｓｉｎθｃｏｓθ
ｓｉｎθ≠０ なので、 ３−４ｓｉｎ2θ＝２ｃｏｓθ より、 ４ｃｏｓ2θ−１＝２ｃｏｓθ
４ｃｏｓ2θ−２ｃｏｓθ−１＝０ において、ｃｏｓθ＞０ なので、 ｃｏｓθ＝（１＋√５）/４
このとき、 ｃｏｓ２θ＝２ｃｏｓ2θ−１＝（３＋√５）/４−１＝（√５−１）/４
よって、与式＝（１/４）（１＋（１＋√５）（√５−１）/１６）＝（１/４）（１＋１/４）＝５/１６
（コメント） 試験本番で、このような計算を短時間で本当に出来るでしょうか？
ＧＡＩ さんからのコメントです。（平成３１年４月２７日付け）
一般に、x＝π/(2*n+1) (n=1、2、3、･･･) とするとき、
Π[k=1,n]sin(k*x)＝√(2*n+1)/2^n
Π[k=1,n]cos(k*x)=1/2^n
が成立しそうです。
実際に、n＝2 では、 sin(π/5)*sin(2π/5)=√5/4 から、
sin(π/5)*sin(2π/5)*sin(3π/5)*sin(4π/5)=(sin(π/5)*sin(2π/5))^2=5/16
同じく、 cos(π/5)*cos(2π/5)=1/4 から、
cos(π/5)*cos(2π/5)*cos(3π/5)*cos(4π/5)
=cos(π/5)*cos(2π/5)*(-cos(2π/5))*(-cos(π/5))
=(cos(π/5)*cos(2π/5))^2=(1/4)^2=1/16
等々のスッキリ値で表して行ける。
らすかるさんからのコメントです。（平成３１年４月２８日付け）
sin(π/5)、sin(2π/5)、−sin(3π/5)、−sin(4π/5) が、
16x^4−20x^2＋5＝0
の４つの解になります。
DD++さんからのコメントです。（平成３１年４月２８日付け）
α = cos(2π/5) + i sin(2π/5) とおく。５次方程式 x^5 = 1 の解は、
x = 1 、α 、α^2 、α^3 、α^4
なので、恒等式 x^5 - 1 = (x-1) (x-α) (x-α^2) (x-α^3) (x-α^4) が成立する。
この両辺を x-1 で割ると、
x^4 + x^3 + x^2 + x + 1 = (x-α) (x-α^2) (x-α^3) (x-α^4)
これに x=1 を代入して、 5 = (1-α) (1-α^2) (1-α^3) (1-α^4)
両辺の絶対値を取って、 5 = |1-α| |1-α^2| |1-α^3| |1-α^4|
右辺のそれぞれの絶対値の意味を、複素数平面上で図形的に考えると、
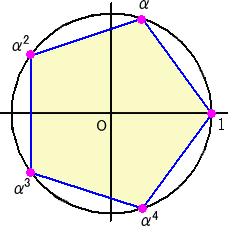
5 = 2sin(π/5) * 2sin(2π/5) * 2sin(3π/5) * 2sin(4π/5)
すなわち、 sin(π/5) sin(2π/5) sin(3π/5) sin(4π/5) = 5/16
理工学部を受験する生徒なら、受験勉強をする中で一度くらいこういう計算をやったことが
あるでしょう。本番で複素数の「ふ」の字もない問題から、これを思い出せた人は時間的に有
利になる、ということなんでしょうね。
（コメント） なるほど！複素数を使えば、難解な計算をしなくても済むわけですね。
