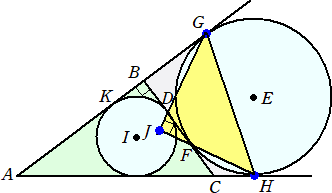
内接円 I と辺BCの接点をDとする。
△ABCの傍接円Eと各辺およびそ
の延長との接点をF、G、Hとする。
また、直線GDと直線HFの交点を
Jとする。
このとき、△GJHは直角2等辺三角形であることを示せ。
GoGeometryの一連のProblem 1407-1411 について、所謂初等幾何でどのように証明した
ものか悩んでおります。
例えば1407は図に描けば合同な直角三角形が4つ現れてなるへそで終わるのですが、そ
んなものが「証明」として認められるのかとつい思ってしまいます。皆様なら如何に解決なさ
るでしょうか。
ハンニバル・フォーチュンさんからのコメントです。(平成31年2月3日付け)
1411 は open problem なのですね。
DD++さんからのコメントです。(平成31年2月3日付け)
合同な直角三角形「3つ」じゃないかと思うんですが、4つめどこにあるんだろう……。これ
1407でいう△BDFに合同な直角三角形、4つどころか6つありますね。
moonlight さんからのコメントです。(平成31年2月6日付け)
そうですね。四つというのは、「2つある円の中心のどちらかを頂点に持つもの」でした。
PBさんからのコメントです。(平成31年2月8日付け)
「1411」の初等幾何的な証明を思いついたのでメールしました。
Problem1411 The figure below shows a right triangle ABC (angle B = 90 degree) with
the incircle I tangent to BC at D. The excircle E corresponding to BC is
tangent to BC and tangent to the extensions of AB and AC at
F, G, and
H, respectively. The extensions of GD and FH meet at J. Prove
that the
triangle GJH is an isosceles right triangle.
 |
∠B=90°の直角三角形ABCの 内接円 I と辺BCの接点をDとする。 △ABCの傍接円Eと各辺およびそ の延長との接点をF、G、Hとする。 また、直線GDと直線HFの交点を Jとする。 |
このとき、△GJHは直角2等辺三角形であることを示せ。 |
|
(証明) 点の名称はそのまま使い、さらに、ABと内接円 I の接点をKとします。
円外の点と、そこを通る2接線の接点、円の中心を結んでできる2つの直角三角形が合
同であること(△EFC≡△EHC …等)、四角形KIDBとBFEGが正方形であることは明ら
かとします。
∠IDC=∠CFE=90°で、(∠ICD+∠ECF)×2=180°より、 △ICD∽△CEF
よって、 ID:DC=CF:FE
また、ID+DC=BD+DC=BC、CF+FE=CF+FB=BC であるから、
ID+DC=CF+FE
加比の理より、 ID:DC=CF:FE から、 (ID+DC)/DC=(CF+FE)/FE
よって、 CD=FE となり、 CD=GE …(1) である。
ところで、 CD⊥AG、GE⊥AG より、 CD//GE …(2)
(1)(2)より、四角形GDCEは平行四辺形(さらに言えば、ひし形)であり、 GJ//EC
∠ACI=∠ICD=∠CEF=∠CHJ (接弦定理) より、 JH//IC であるから、
∠ECI=90°より、 ∠GJH=90°…(3)
また、 ∠GEF=90°で、∠GHFは、弧GFに対する円周角なので、
∠GHF=45°…(4)
(3)(4)より、△GJHは直角二等辺三角形である。 (証終)
(コメント) 素晴らしい初等的な証明ですね!PBさんに感謝します。
