の問題傾向から大幅に改善された問題が出題された。
その中で、通常の問題とは異なる問いかけをしている、次の問題に興味を持った。
問題 (改題)
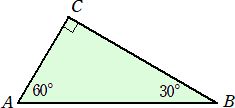
下図のようなAB=20の直角三角形ABCがある。頂点A、B、C上に動点P、Q、Rがあり、
同時に各頂点を出発し、それぞれ一定の速さで辺上を時計回りに次の頂点に移動し、同時
に頂点に着いたという。
点Pの速さを毎秒1とし、△APQ、△BQR、△CRPの面積をそれぞれS1、S2、S3とする
とき、S1、S2、S3にはどのような大小関係が成り立つか、答えよ。
(解) 題意より、Q、Rの速さは、それぞれ毎秒 2t、
t 秒後のS1、S2、S3の面積を求めると、
S1=(1/2)t(20−2t)・(
S2=(1/2)(10−t)・
S3=(1/2)・2t(10
したがって、常に S1=S2=S3 が成り立つ。
(コメント) 同時に頂点を出発し、同時にもう一方の頂点に着くことから、正三角形を考え、
その辺上を3点P、Q、Rが同じ速さで移動すると考えれば、これは当然の帰結
なのかな!
GAI さんからのコメントです。(平成30年11月14日付け)
上記の問題を、すべての数値と、対象とする三角形は同じとして、点P、Q、Rを反時計回り
に移動させるに変更してみて計算したら、結論は、やはり、t 秒後の面積は、それぞれ
√3/8*t^2 となり、S1=S2=S3 が常に成立していました。
従って、別に、元の△ABCは特別な直角三角形でもなく任意の形のものでよく、ただ3つの
動点が同時出発、同時到着の条件さえあれば、この関係式はどちら周りの移動であっても
常に成立しそうですね。ケプラーさんあたりは既にこれに気づいていたのかも。
(コメント) この問題は、実際の問題のごく一部で、最後の方では、GAI さんがご指摘されて
いるような方向で設問されていました。問題を見て半信半疑で計算してみると、確
かに美しく、S1=S2=S3 となるんですね!これには本当に驚きました。
らすかるさんからのコメントです。(平成30年11月14日付け)
任意の三角形は適当な方向に高々2回拡大縮小すれば、3つの三角形の面積が等しいと
いう条件を崩すことなく正三角形に変形できますので、上記で書かれているように「当然の
帰結」ですね。
# 例えば、問題の△ABCは、AB方向に√(3/7)倍に縮小すると、AB=BCの二等辺三角形に
なり(このとき3つの三角形の面積は全て√(3/7)倍になる)、その後、(変形後の)AC方向に
√(7/3)倍に拡大すると正三角形になります。
(3つの三角形の面積は全て√(7/3)倍になり、元の面積と同じ)
DD++さんからのコメントです。(平成30年11月15日付け)
実は、三角形の変形すら必要ありませんね。三角形の面積公式 S=(1/2)*b*c*sinA という
公式は、「同じ角を持つ三角形同士の面積比は、その角を挟む辺のそれぞれの比の積にな
る」ことを保証します。
(この公式を用いなくても補助線を一本引けば簡単に証明できるので、高校入試でもよく出
てくる印象)
つまり、問われている三角形の面積はいずれも「△ABC の t/10 * (10-t)/10 倍」で計算す
ることができ、最初に立てる式が同じなのだから答えも同じ、でおしまいです。
もちろん、この 10 は到着にかかる時間ですが、ここが他の数字に変わっても明らかに定
性的には影響ありません。
