次の三角形は、ただ単純に面白いと思う。∠Ａの大きさが∠Ｂの大きさの２倍になるから
だ。そんな三角形は直角三角形だったら簡単に作れるが、そうでなく一般の三角形である
ところがいい。しかも、その証明は数学Ａの平面図形の問題として適当である。

　皆さんは、∠Ａ＝２∠Ｂ　が証明できるだろうか？挑戦してみては如何？

　　　


（解）　∠Ｃの２等分線が辺ABと交わる点をＤとし、ＢＣ上の点ＥをAC＝EC＝９　であるよう
　　　にとる。

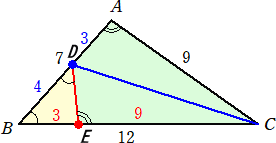ＣＤは∠Ｃの２等分線なので、 　　AD ： DB＝CA ： ＣＢ＝９ ： １２＝３ ： ４ 　　AB＝７　より、　ＡＤ＝３、ＤＢ＝４　となる。 　このとき、△CAD≡△CED　から、DE＝AD＝３

　　　　　　　　また、BE＝３　から、△EBDはEB＝EDの２等辺三角形なので、∠Ｂ＝∠EDB

　　　　　　　よって、　　∠A＝∠CED＝∠Ｂ＋∠EDB＝２∠Ｂ　　（終）


　Ｓ（Ｈ）さんからのコメントです。（平成３０年１１月１０日付け）

　Ｂ（0，0）、Ｃ（12，0）　とし、ｘ² + ｙ² = ７²　、(ｘ - 12)² + ｙ² = ９²　から、Ａ(14/3，7/3)

　このとき、　AC・AB = (22/3，-7/3)・(-14/3，-7/3)=-7

　　　　　また、　AC・AB = 9*7*ｃｏｓＡ　なので、　ｃｏｓＡ = -1/9

　ところで、　ｔａｎＢ = (7/3)/(14/3)=/2

　ここで、ｃｏｓ２Ｂ = ｃｏｓ²Ｂ - ｓｉｎ²Ｂ = ｃｏｓ²Ｂ（1 - ｔａｎ²Ｂ） = （1 - ｔａｎ²Ｂ）/（1 + ｔａｎ²Ｂ）

なので、ｃｏｓ２Ｂ = -1/9 となる。すなわち、ｃｏｓ２Ｂ = ｃｏｓＡ　である。

　Ａは鈍角で、Ａ、Ｂは△ABCの内角より、　A + ２Ｂ ≠ ２π　なので、　２Ｂ＝Ａ　となる。


　ＧＡＩ さんからのコメントです。（平成３０年１１月７日付け）

　上記のような「∠A=2∠B」の関係を生み出す(a,b,c)=(12,9,7)以外の△ABCの形状を調べ
てみた。

(a,b,c)=(6,4,5)、(15,9,16)、(20,16,9)、(28,16,33)、(30,25,11)、(35,25,24)、(40,25,39)、(42,36,13)
　　　　(45,25,56)、(56,49,15)、(63,49,32)、(66,36,85)、(70,49,51)、(72,64,17)、(77,49,72)
　　　　(84,49,95)、(88,64,57)、(90,81,19)、(91,49,120)、(99,81,40)、･･･････

　また、「∠A=3∠B」の関係を生み出す△ABCの形状を調べてみたら、

(a,b,c)=(10,8,3)、(48,27,35)、(132,64,119)、(195,125,112)、･･･････


　らすかるさんからのコメントです。（平成３０年１１月７日付け）

　「∠A=2∠B」を満たすaの数列は、「A106430」にありました。

　ところで、その結果を眺めていると、bは常に平方数になっていますね。これは、少し考えた
ら必ず平方数になることが簡単に示せました。つまり、

　∠A=2∠B を満たす整数辺三角形で、GCD(a,b,c)=1　ならば　b は平方数

が成り立ちます。


　よおすけさんからのコメントです。（平成３０年１１月７日付け）

　「∠A=n∠B」のとき、辺の長さCA(=b)はn乗数なのかな？　（※nは正の整数）


　らすかるさんからのコメントです。（平成３０年１１月８日付け）

　そうなりそうです。一般のｎに対して、a、b、c の間に成り立つ式を、f[n](a,b,c)=0 として、
n=6 まで求めてみると、

f[1](a,b,c)=a-b

f[2](a,b,c)=a^2-b^2-bc

f[3](a,b,c)=a^3-a^2b-ab^2+b^3-bc^2

f[4](a,b,c)=a^4-2a^2b^2+b^4-a^2bc+b^3c-b^2c^2-bc^3

f[5](a,b,c)=a^5-a^4b-2a^3b^2+2a^2b^3+ab^4-b^5-a^2bc^2-ab^2c^2+2b^3c^2-bc^4

f[6](a,b,c)=a^6-3a^4b^2+3a^2b^4-b^6-a^4bc+2a^2b^3c-2a^2b^2c^2
　　　　　　　　　　　　　　　　　　　　　　　　　　-a^2bc^3-b^5c+2b^4c^2+2b^3c^3-b^2c^4-bc^5

のようになりますが、この式を見ると、少なくとも 1＜n≦6 では、b がｎ乗数になっていなけ
ればいけないことがわかります。（簡単に証明できます。）

　また、これらの式をじっくり眺めると、

f[0](a,b,c)=1

f[1](a,b,c)=a-b

f[n](a,b,c)=(a+b(-1)^n+c)f[n-1](a,b,c)-(ac)f[n-2](a,b,c)

という三項間漸化式が、（n≦6の範囲では）成り立つことがわかります。もし、この漸化式が
n＞6でも成り立てば、bがn乗数であることは間違いないことになりますが、今のところその
証明はできていません。


　ＧＡＩ さんからのコメントです。（平成３０年１１月８日付け）

　∠A=4∠B での△ABCでの辺(a,b,c)が、

(a,b,c)=(105,81,31)、(476,256,305)、(1395,625,1111)、(3234,1296,2869)、(3864,2401,1969)、
･････････････････

のとき、そのような関係を持つので多分間違いないでしょうね。角度では倍数なのに、辺で
は累乗になるなんて面白いですね。