な問題をいくつか紹介したい。
問題1 8進法で4桁の自然数 m=abcd(8) がある。このとき、2mも8進法で4桁の自然
数で、数字の並びがmと逆になるという。すなわち、2m=dcba(8) である。
このようなmをすべて求めよ。
(解) 題意より、 m=a・83+b・82+c・8+d と書かれるので、
2m=2a・83+2b・82+2c・8+2d
=d・83+c・82+b・8+a
2mは、8進法で4桁なので、 a=1、2、3
また、 2d=a または、 2d−8=a で何れにしても aは偶数なので、 a=2
このとき、 2d=2 または、 2d−8=2 なので、 d=1 または d=5
ところで、 d=2a または d=2a+1 なので、 d=1 は不適
よって、 d=5
また、 2bー8=c または 2b+1−8=c
2c+1=b または 2c+1−8=b
まず、2bー8=c、2c+1=b のとき、 4b−16+1=b より、 b=5、c=2
2bー8=c、2c+1−8=b のとき、 4b−16−7=b を満たす自然数解はなし
2b+1−8=c、2c+1=b のとき、 4b−14+1=b を満たす自然数解はなし
2b+1−8=c、2c+1−8=b のとき、 4b−14−7=b より、 b=7、c=7
以上から、求める自然数は8進法で、 2525(8) 、2775(8) の2つである。 (終)
問題2 8進法で2桁の自然数 m=ab(8) がある。このとき、2mも8進法で2桁の自然数
で、数字の並びがmと逆になるという。すなわち、2m=ba(8) である。
このとき、このようなmをすべて求めよ。
(解) 題意より、 m=a・8+b と書かれるので、
2m=2a・8+2b=b・8+a
2mは、8進法で2桁なので、 a=1、2、3
また、 2b=a または、 2b−8=a で何れにしても aは偶数なので、 a=2
このとき、 2b=2 または、 2b−8=2 なので、 b=1 または b=5
ところで、 b=2a または b=2a+1 なので、 b=1 は不適
よって、 b=5
以上から、求める自然数は8進法で、 25(8) のみである。 (終)
問題3 8進法で3桁の自然数 m=abc(8) がある。このとき、2mも8進法で3桁の自然数
で、数字の並びがmと逆になるという。すなわち、2m=cba(8) である。
このとき、このようなmをすべて求めよ。
(解) 題意より、 m=a・82+b・8+c と書かれるので、
2m=2a・82+2b・8+2c=c・82+b・8+a
2mは、8進法で3桁なので、 a=1、2、3
また、 2c=a または、 2c−8=a で何れにしても aは偶数なので、 a=2
このとき、 2c=2 または、 2c−8=2 なので、 c=1 または c=5
ところで、 c=2a または c=2a+1 なので、 c=1 は不適
よって、 c=5
また、 2b+1ー8=b より、 b=7
以上から、求める自然数は8進法で、 275(8) のみである。 (終)
問題4 8進法で5桁の自然数 m=abcde(8) がある。このとき、2mも8進法で5桁の自
然数で、数字の並びがmと逆になるという。すなわち、2m=edcba(8) である。
このとき、このようなmをすべて求めよ。
(解) 題意より、 m=a・84+b・83+c・82+d・8+e と書かれるので、
2m=2a・84+2b・83+2c・82+2d・8+2e
=e・84+d・83+c・82+b・8+a
2mは、8進法で5桁なので、 a=1、2、3
また、 2e=a または、 2e−8=a で何れにしても aは偶数なので、 a=2
このとき、 2e=2 または、 2e−8=2 なので、 e=1 または e=5
ところで、 e=2a または e=2a+1 なので、 e=1 は不適
よって、 e=5
また、 2bー8=d または 2b+1−8=d
2d+1=b または 2d+1−8=b
2c=c または 2c−8=c または 2c+1−8=c
第3行より、 c=0 または c=8 または c=7
また、2bー8=d、2d+1=b のとき、 4b−16+1=b より、 b=5、d=2
このとき、 2c=c より、 c=0
2bー8=d、2d+1−8=b のとき、 4b−16−7=b を満たす自然数解はなし
2b+1−8=d、2d+1=b のとき、 4b−14+1=b を満たす自然数解はなし
2b+1−8=d、2d+1−8=b のとき、 4b−14−7=b より、 b=7、d=7
このとき、 2c+1−8=c より、 c=7
以上から、求める自然数は8進法で、 25025(8) 、27775(8) の2つである。 (終)
#自信がなかったので、確かめてみました。
25025(8)×2=52052(8) 、27775(8)×2=57772(8)
次の問題は上記と同趣旨の問題と思われるが、解法は少し異なるようである。
問題5 ある自然数Nを5進法で表すと3桁の数abc(5)となり、3倍して9進法で表すと3桁
の数cba(9)となる。a、b、cの値を求めよ。
(解) 題意より、 N=a・52+b・5+c と表されるので、 3N=75a+15b+3c
ところで、 3N=c・92+b・9+a=81c+9b+a なので、
75a+15b+3c=81c+9b+a すなわち、74a+6b=78c より、 37a+3b=39c
a=1、2、3、4 で、aは3の倍数なので、 a=3
よって、 37+b=13c
b=0、1、2、3、4 で、37+bが13の倍数となるのは、 b=2
よって、 c=3 (終)
問題6 1を1つ、2を2つ、・・・、9を9つ用いて10進表記される自然数は、平方数でないこ
とを示せ。
(解) 1を1つ、2を2つ、・・・、9を9つ用いて10進表記される自然数をNとすると、
N≡12+22+32+42+52+62+72+82+92=9・10・19/6=285≡6 (mod 9)
Nが平方数になると仮定すると、Nを9で割った余りは、0、1、4、7 の何れか。
これは矛盾。
よって、Nは平方数でない。 (終)
問題7 1を2つ、2を2つ、3を2つ、4を2つ用いて10進表記される自然数は、平方数でな
いことを示せ。
(解) 1を2つ、2を2つ、3を2つ、4を2つ用いて10進表記される自然数をNとすると、
N≡1×2+2×2+3×2+4×2=20≡2 (mod 9)
Nが平方数になると仮定すると、Nを9で割った余りは、0、1、4、7 の何れか。
これは矛盾。
よって、Nは平方数でない。 (終)
問題8 5進法で書かれた数xが偶数か奇数かは、各位の数の和から判断できることを示せ。
(解) 5進法で書かれた数 x=anan-1・・・a1a0(5) は、10進法で表すと、
x=an・5n+an-1・5n-1+・・・+a1・5+a0
これを、2を法とする合同式で考えると、nを自然数として、 5≡1 から、5n≡1
よって、 x≡an+an-1+・・・+a1+a0 (mod 2) より、x の偶奇は、各位の数の
和から判断できる。 (終)
問題9 2018!を10進法で表すと、後ろの方の桁に0がいくつか並ぶ。1の位から見てい
き、最初に現れる0でない数は偶数であることを示せ。
(解) 2018!に含まれる5の個数は、
2018÷5=403・・・3
403÷5=80・・・3
80÷5=16
16÷5=3・・・1
より、全部で 403+80+16+3=502(個)ある。
2の個数はもっと多いので、2018!を10進法で表すと、後ろの方の桁に0が502(個)
並ぶ。
ところで、2018!に含まれる2の個数は、
2018÷2=1009
1009÷2=504・・・1
504÷2=252
252÷2=126
126÷2=63
63÷2=31・・・1
31÷2=15・・・1
15÷2=7・・・1
7÷2=3・・・1
3÷2=1・・・1
より、全部で2011個ある。10を作るために502個使っても、まだ1509個も2が残るので、
1の位から見ていき、最初に現れる0でない数は偶数であることが分かる。 (終)
問題10 1、2、3、4、5、6 を並べ替えて6桁の整数を作る。作った6桁の整数の上2桁は
2の倍数、上3桁は3の倍数、上4桁は4の倍数、上5桁は5の倍数、上6桁は6の倍
数になるようにするには、6個の数字をどう並べればよいか。
(出典:聖光学院中学入試問題)
(解) 6桁の整数を、(ア)(イ)(ウ)(エ)(オ)(カ) とする。
まず、(ア)(イ)(ウ)(エ)(5)(カ) であることは明らか。
次に、(イ)、(エ)、(カ)は偶数 2、4、6 の何れかが入るので、(ア)、(ウ)には、1また
は3の何れかが入る。
(1)(イ)(3)(エ)(5)(カ) の場合
まず、(1)(イ)(3)(2)(5)(カ) とすると、(イ)は、4または6だが、何れも3の倍数になら
ない。
(1)(2)(3)(6)(5)(4) ・・・ 適する
(3)(イ)(1)(エ)(5)(カ) の場合
まず、(3)(イ)(1)(2)(5)(カ) とすると、(イ)は、4または6だが、何れも3の倍数になら
ない。
(3)(2)(1)(6)(5)(4) ・・・ 適する
以上から、 123654 または 321654 (終)
問題11 数学セミナー ’18 12月号(日本評論社)の「エレガントな解答をもとむ」の9月
号出題の問題の解答で、次の事実が証明されている。
任意の自然数nに対して、nの倍数で、各位の数の和がちょうどnである十進法の
数が存在する
例 n=1〜9 は自明
n=10 のときは、すぐ思いつくのは、11111111110 かな...。でも、「190」とした
方が桁数も少ないし、数としても最小っぽい。
n=11 のときは、209=11×19 が最小解である。
n=12 のときは、48=12×4 が最小解である。
そこで、問題です。n=13のとき、そのような数の最小値を求めて下さい。
(解) 247 (終)
(コメント) オンライン整数列辞典の「A002998」で既に解が調べられていますね!
n=14 のときは、266
n=15 のときは、195
n=16 のときは、448
n=17 のときは、476
n=18 のときは、198
n=19 のときは、874
n=20 のときは、3980
・・・・・・・・・・・・・・・・・・・・・
問題12 連続する2つの自然数の積で、1が連続して3つ並ぶものを見つけよ。
(解) 31×36=1116 もそうだが、 3×37=111 の方が有名かも!
問題13 連続する3つの自然数の積で、1が連続して4つ並ぶものを見つけよ。
(解) 1035×1036×1037=1111933620
類題として、「1が99個以上並ぶものを見つけよ。」が、東京大学 理系(2013年)で出題
されている。
東京大学 理系(2013年)
次の命題Pを証明したい。
命題P 次の条件(a)、(b)をともに満たす自然数(1以上の整数)Aが存在する。
(a) Aは連続する3つの自然数の積である。
(b) Aを10進法で表したとき、1が連続して99回以上現れるところがある。
以下の問いに答えよ。
(1) yを自然数とする。このとき、不等式
x3+3yx2<(x+y−1)(x+y)(x+y+1)<x3+(3y+1)x2
が成り立つような正の実数xの範囲を求めよ。
(2) 命題Pを証明せよ。
(解)(1) A=(x+y−1)(x+y)(x+y+1)=(x+y)3−x−y
=x3+3yx2+3xy2+y3−x−y
B=x3+3yx2
C=x3+(3y+1)x2 とおく。
まず、A−B=3xy2+y3−x−y=(3y2−1)x+y(y−1)(y2+y+1)>0
題意より、 y≧1 なので、 3y2−1≧2>0 、 y(y−1)(y2+y+1)≧0
よって、正の実数xについて、A−B>0は常に成り立つ。
次に、C−A=x2−3xy2−y3+x+y=x2−(3y2−1)x−y(y−1)(y2+y+1)>0
x=0 のとき、−y(y−1)(y2+y+1)≦0 なので、xの2次方程式
x2−(3y2−1)x−y(y−1)(y2+y+1)=0 は、α≦0≦βなる2実数解α、βを持つ。
α+β=3y2−1≧2>0 なので、α≦0<βなる2実数解α、βを持つ。
よって、C−A>0 の解は、x>0に注意して、 x>β となる。
すなわち、 x>[3y2−1+√{(3y2−1)2+4y(y−1)(y2+y+1)}]/2
(2) a=1・・・99個・・・1 とおくと、
a=1110・・・96個・・・0+1110・・・93個・・・0+・・・・+111000+111
=111×(10・・・96個・・・0+10・・・93個・・・0+・・・+1000+1)
=3×37×(10・・・96個・・・0+10・・・93個・・・0+・・・+1000+1)
なので、aは3の倍数で、 a=3y (yは自然数) と書ける。
すなわち、 3y=1・・・99個・・・1 である。
このとき、 3y<1099 より、 y<1099 なので、x=10200 とすれば、
(3y2−1)x+y3−y<3y2x+y3=y2(3x+y)<10198(3・x+1099)<10400=x2
を満たす。
よって、 命題Pの条件(a)、(b)をともに満たす自然数(1以上の整数)Aは、
x=10200 、3y=1・・・99個・・・1 とおくとき、
連続する3つの自然数の積(x+y−1)(x+y)(x+y+1)として、
B=x3+3yx2=10600+1・・・99個・・・1×10400
=10・・・101個・・・01・・・99個・・・10・・・400個・・・0
C=x3+(3y+1)x2=10・・・101個・・・01・・・98個・・・120・・・400個・・・0
より、 A=10・・・101個・・・01・・・99個・・・1*・・・400個・・・* (*は、0〜9の数字) と書
けて、確かに存在する。 (終)
(コメント) 上記の問題を活用して、「連続する3つの自然数の積で、1が連続して3つ並ぶ
もの」を構成してみよう。
a=111 とおくと、 a=3×37 で、aは3の倍数で、 a=3y (y=37) と書ける。
すなわち、 3y=111 である。
このとき、 3y<104 、 y<102 なので、x=105 とすれば、
(3y2−1)x+y3−y<3y2x+y3=y2(3x+y)<104(3・x+102)<1010=x2
を満たす。
よって、 x=105 、y=37 とおくとき、連続する3つの自然数の積は、
(x+y−1)(x+y)(x+y+1)
=100036・100037・100038=1001110410650620
となる。
問題 3999991は素数でないことを示せ。
(解) 3999991=4000000−9=20002−32=2003・1997 と因数分解されるの
で素数でない。 (終)
(類題) 9991は素数でないことを示せ。
(解) 9991=10000−9=1002−32=103・97 と因数分解されるので素数でない。
(終)
(追記) 平成31年1月11日付け
問題 △ABCにおいて、tanA、tanB、tanC が何れも整数になるとき、その値を求めよ。
(出典:一橋大学(1984))
(解) A+B+C=180°なので、少なくとも一つは60°以下である。その角をAとする。
このとき、 0<tanA≦
tanA=tan(180°−B−C)=−tan(B+C)=−(tanB+tanC)/(1−tanB・tanC)=1
より、 tanB・tanC−tanB−tanC=1 すなわち、
(tanB−1)(tanC−1)=2
tanB、tanC は整数なので、取り得る値は、 2 または 3
以上から、tanA、tanB、tanC の取り得る値は、 1、2、3
(コメント) tanA=1、tanB=2、tanC=3 となる三角形を実際に作図したいのだが、結構
難しい。
当HPがいつもお世話になっているHN「PB」さんからのコメントです。
(平成31年1月11日付け)
上記の三角形を作図してみました。
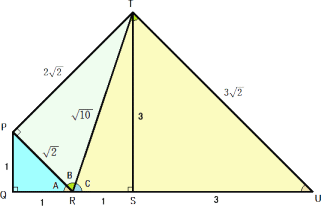
上図のように、PQ=QR=RS=1、TS=3、PQ⊥QS、QS⊥ST とすれば、3つの角は
tanA=1、tanB=2、tanC=3 を満たします。
(PからTSに垂線P’を引けば、PP’=TP’=2 なので、TP=2√2、PR=√2、TR=√10
から、TP⊥PRで、tanB=2 となる)
よって、PR//TU としたときの △TRU すなわち、a=√10、b=4、c=3√2 である
三角形が条件を満たします。
(コメント) なるほど!綺麗に作図できるんですね。PBさんに感謝します。
