乮嶲峫暥專乯丂庴尡嶼悢偵僠儍儗儞僕丂丂嶼悢惎恖偺倂俤俛栤戣廤
丂嶰妏宍俙俛俠偼丄俙俠亖侾俋/俀們倣偱丄柺愊偑侾俆們噓 偱偡丅俛俠偺拞揰傪俢偲偡傞偲丄
佢俙俢俠亖侾俁俆亱偵側傝傑偟偨丅偙偺偲偒丄俙俛偺挿偝偼丄壗們倣偱偡偐丠
丂丂丂丂丂丂
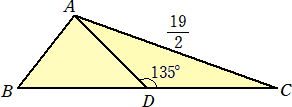
丂俽乮俫乯偝傫偵傛傟偽丄嵗昗傪愝偗偰丄A(倶丆倷)丄俛(0丆0)丄俠(a丆0)丄a = BC丄俙俛 = r丂偲偟丄
丂x^2 + y^2 = r^2丂丄丂(x - a)^2 + y^2=(95/10)^2丂丄y = Tan[135亱]*(x - a/2)}
偝傜偵丄 s = (r + a + 95/10)/2 偲偍偒丄柺愊 = 15 偐傜丄s(s - a)(s - 95/10)(s - r)] = 225
丂偙傟偐傜丄 r 偲 a 傪媮傔偰丄丂r = AB = 11/2丂偲側傞丅
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俁侽擭俋寧侾擔晅偗乯
丂搨撍偵柺愊偑彂偄偰偁傞偲偄偆偙偲偼丄恾宍暲傋懼偊宯偩傠偆偲偄偆偙偲偲丄挿偝偑1売強偟
偐傢偐傜側偄偺偱丄惓曽宍偔傜偄偟偐嶌傟偦偆偵側偄偲偄偆偙偲偐傜丄偲傝偁偊偢丄捈妏嶰妏
宍偵傇偭偨愗傟偽傛偝偦偆偩偲敾抐丅
丂恾偑俀庬椶嶌傟傞偺偱屄暿偵丏丏丏丅
(i)丂AD亙CD 偺応崌
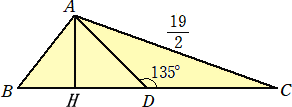
丂揰 A 偐傜曈 BC 偵悅慄傪堷偒丄偦偺懌傪 H 偲偟傑偡丅仮ABC 偼 仮ABH 偲 仮ACH 偵暘
妱偝傟傑偡丅
丂丂丂丂丂
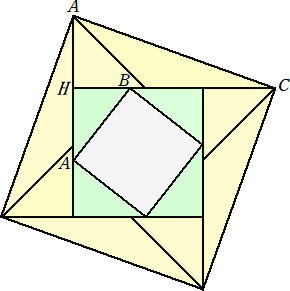
丂偙傟傜俀庬椶偺捈妏嶰妏宍偺斅傪 4 枃偢偮梡堄偟傑偡丅
丂仮ACH 宆偺斅 4 枃傪丄9.5 cm 偺曈偑偦傟偧傟惓曽宍偺奜廃偵側傞傛偆偵 90亱偢偮岦
偒傪曄偊偰暲傋傑偡丅偙偺偲偒丄撪晹偵惓曽宍偺寗娫偑偱偒傑偡偑丄偦偺曈偺挿偝偼丄
丂丂CH-AH = CH-DH = CD = BD = BH+DH = BH+AH
乮佹佢ADH=45亱 側偺偱丄仮ADH 偼捈妏擇摍曈嶰妏宍偱丄AH=DH 乯
丂偮傑傝丄仮ABH 偺捈妏傪嫴傓俀曈偺挿偝偺榓偵側偭偰偄傞偺偱丄係枃偺 仮ABH 宆偺斅傪
捈妏傪寗娫偺妏偵崌傢偣傞傛偆偵 90亱偢偮岦偒傪曄偊偰抲偄偰偄偔偲丄嵞傃撪晹偵惓曽宍
偺寗娫偑偱偒傑偡丅
丂丂丂丂丂
丂偦偺曈偺挿偝偼 AB 偵摍偟偄偱偡偑丄堦曽偱丄偙偺惓曽宍偺寗娫偺柺愊偼丄
丂丂9.5*9.5 - 15*4 = 90.25 - 60 = 30.25 = 5.5*5.5 cm^2
側偺偱丄AB 偺挿偝偼 5.5 cm 偲傢偐傝傑偡丅
(ii)丂AD亜CD 偺応崌
丂丂丂丂丂
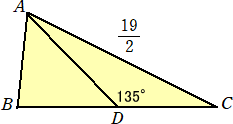
丂偙偺嶰妏宍傪慄暘 AD 偱愗抐偟丄仮ABD 偩偗傪揰 D 傪拞怱偵 180亱 夞揮偝偣傑偡丅偡傞
偲丄(i) 偲摨堦偺恾宍偵側傞偺偱丄AB 偺挿偝偼 5.5 cm 偲傢偐傝傑偡丅
丂偄偢傟偵偣傛丄AB 偺挿偝偼 5.5 cm 偱偡丅
乮僐儊儞僩乯丂DD++偝傫偺傾僀僨傾偼慺惏傜偟偄偱偡偑丄側偐側偐婥偯偒偵偔偄偱偡偹両曽掱
丂丂丂丂丂丂幃傪棫偰偰夝偄偰傒傑偟偨丅
丂丂丂丂丂

乮夝乯丂俙俫亖倶丄俛俢亖俠俢亖倷丂偲偍偔偲丄仮俙俛俠偺柺愊偑侾俆偱偁傞偙偲偐傜丄
丂丂丂乮侾/俀乯丒俀倷丒倶亖倶倷亖侾俆
丂傑偨丄仮俙俫俠偵偍偄偰丄嶰暯曽偺掕棟傛傝丄丂倶2亄乮倶亄倷乯2亖乮侾俋/俀乯2亖俁俇侾/係
丂偡側傢偪丄丂俀倶2亄倷2亄俀倶倷亖俁俇侾/係丂傛傝丄丂俀倶2亄倷2亖俀係侾/係
丂傛偭偰丄丂俙俛2亖倶2亄乮倷亅倶乯2亖俀倶2亄倷2亅俀倶倷亖俀係侾/係亅俁侽亖侾俀侾/係丂傛傝丄
丂丂俙俛亖侾侾/俀丂丂乮廔乯
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
