問 半径1の球面上の4地点をリアルタイムで観測するため、球面からの高度が1の軌道に
静止衛星を周回させるとき、4地点が球面上のどこにあっても常に観測できるようにする
には、少なくとも何台の静止衛星が必要か。
ただし、各地点は球面上の定点である。ここで静止衛星とは、球面に対する相対的な
位置関係が常に一定である点とし、静止衛星Sから球面上のある地点Pが観測されると
は、線分SPと球面の共有点が点P以外に存在しないことをいうものとする。
らすかるさんからのコメントです。(平成30年8月24日付け)
静止衛星は赤道面上にしか存在し得ませんので、4地点のうちの1地点が北極付近または
南極付近の場合は静止衛星が何台あっても観測できないと思います。
DD++さんからのコメントです。(平成30年8月24日付け)
単純に重力と遠心力で釣り合わせる静止衛星は赤道上空 36000km にしか設置できませ
んが、動力を利用して極方向への力を生み出し強引に位置を合わせ続ける方法なら、赤道
上以外にも静止衛星(この問題の定義で)は設置できます。
現実世界では絶対にやらないと思いますが、とりあえず数学の問題においては、らすかる
さんの指摘は不適当ではないかと思います。
で、答えは「2基」ですかね。4地点を A, B, C, D として、
・AとB、CとD、をそれぞれ1基の衛星で観測する
・AとC、BとD、をそれぞれ1基の衛星で観測する
・AとD、BとC、をそれぞれ1基の衛星で観測する
のいずれも不可能な場合、必ず1基の衛星で4地点中3地点を観測することが可能です。
ところで、この2基を「必ず球の対称位置に設置すること」という条件をつけた場合でも、任
意の4点に対して観測可能な設置方法が必ず存在するのでしょうかね?
とりあえず私には反例になりそうな点配置はパッと思いつきませんが……。
らすかるさんからのコメントです。(平成30年8月24日付け)
例えば、
(x,y,z)=(cos2°,sin2°,0),(cos61°,sin61°,0),(cos119°,sin119°,0),(cos178°,sin178°,0)
の4点にした場合は不可能では?
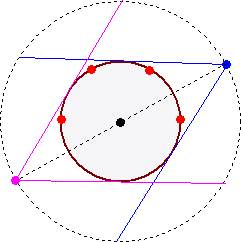
DD++さんからのコメントです。(平成30年8月25日付け)
おお、なるほど、確かに。両方の衛星で手分けして観測するのは不可能ですが、1つの衛
星では3つまでしか入らないですね。
(コメント) 1つの衛星から球面を見込む角の大きさは、60°すなわち、らすかるさんの例
だと、1つの衛星でカバーできる地点は最大3点までなんですね。そうすると、その
対称位置にある衛星で残りの1地点は観測できない。
ハンニバル・フォーチュンさんからのコメントです。(平成30年8月24日付け)
みかづきさんは三次元の接吻数からこの問題の題材を得たのかと当初感じましたが、皆
様の論議を拝見いたしますと、どうも違うようです...とほほ。
