２つ以上の数の共通の倍数を公倍数といい、その中で最小の数が最小公倍数（ＬＣＭ）
と言われる。

　同様に、２つ以上の数の共通の約数を公約数といい、その中で最大の数が最大公約数
（ＧＣＭ）と言われる。

　２つの数 Ａ、Ｂ に対して、その最大公約数をＧ、最小公倍数をＬとすると、次の公式がよく
知られている。

　Ａ＝Ａ’Ｇ　、Ｂ＝Ｂ’Ｇ　　（　Ａ’、Ｂ’は互いに素）　、Ｌ＝Ａ’Ｂ’Ｇ　、　ＬＧ＝ＡＢ

＜具体的な計算例＞

（１）　２０と２４の最大公約数と最小公倍数を求めよ。

（方法１）　　２０＝２²×３⁰×５¹　、２４＝２³×３¹×５⁰　から、　Ｇ＝２²×３⁰×５⁰＝４　、

　　　　　　Ｌ＝２³×３¹×５¹＝２³×３×５＝１２０

（方法２）　２０＝２²×５　、２４＝２³×３　から、　Ｇ＝２²＝４　、

　　　　　　Ｌ＝２²×５×（２×３）＝２³×３×５＝１２０

（方法３）　２０＝２²×５　、２４＝２³×３　から、　Ｇ＝２²＝４　、

　　　　　　Ｌ＝（２²×５）×（２³×３）/２²＝２³×３×５＝１２０

（方法４）
　　　　　　　　　　　

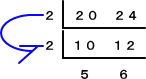
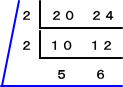
　　　　　上記の計算から、　Ｇ＝２×２＝４　、Ｌ＝２×２×５×６＝１２０

（方法５）　互除法を利用して、Ｇを求め、（方法２）の方法でＬが求められる。

　　　　　　

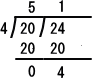
　　　　上記により、Ｇ＝４　で、Ｌ＝１２０　となる。

（２）　２０と２４と３０の最大公約数と最小公倍数を求めよ。

（方法１）　２０＝２²×３⁰×５¹　、２４＝２³×３¹×５⁰　、３０＝２¹×３¹×５¹　から、

　　　　　Ｇ＝２¹×３⁰×５⁰＝２　、Ｌ＝２³×３¹×５¹＝１２０

（方法２）　３つの数の最小公倍数の計算には次の手順が必要となる。

　　　ＬＣＭ｛ａ，ｂ，ｃ｝＝ＬＣＭ｛ＬＣＭ｛ａ，ｂ｝，ｃ｝

　（１）より、ＬＣＭ｛２０，２４｝＝１２０　なので、ＬＣＭ（１２０，３０｝＝１２０

　また、Ｇ＝２　は明らかであろう。

（方法３）　（方法２）から分かるように、筆算でＧ、Ｌを求める場合には注意が必要である。

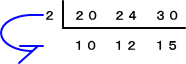　　　　　　から、　Ｇ＝２

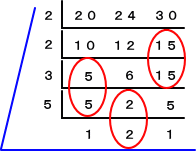　　　　　　から、　Ｌ＝２×２×３×５×１×２×１＝１２０


　４数の場合についても上記の筆算が有効であることを見ておこう。

（３）　２０と２４と３０と４２の最大公約数と最小公倍数を求めよ。

（方法１）　２０＝２²×３⁰×５¹×７⁰　、２４＝２³×３¹×５⁰×７⁰　、３０＝２¹×３¹×５¹×７⁰

　　　　　　４２＝２¹×３¹×５⁰×７¹　から、

　　　　　Ｇ＝２¹×３⁰×５⁰×７⁰＝２　、Ｌ＝２³×３¹×５¹×７¹＝８４０

（方法２）　
　　　　　　から、　Ｇ＝２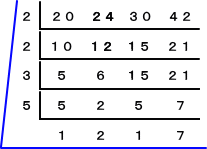

　　　　　　から、　Ｌ＝２×２×３×５×１×２×１×７＝８４０



　　以下、工事中！