「与えられた立方体の２倍の体積を持つ立方体を作図する」（立方体倍積問題）ことは
不可能である。これは、が定木とコンパスで作図出来ないからである。ところが、折り紙
だったら、実は、を作図することができる。

　この話題について、まとめたいと思う。

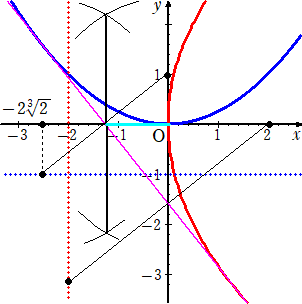
　焦点（０，１）、準線 ｙ＝−１の放物線Ｃ₁： ４ｙ＝ｘ² と焦点（２，０）、準線 ｘ＝−２の放物線
Ｃ₂： ｙ²＝８ｘ を考え、２つの放物線に共通接線を引く。

　放物線Ｃ₁上の接点の座標を（ｐ，ｑ）とおくと、接線の方程式は、２（ｙ＋ｑ）＝ｐｘ　と書ける。

この接線が放物線Ｃ₂にも接するので、　ｙ²＝８・２（ｙ＋ｑ）/ｐ　即ち、ｐｙ²−１６ｙ−１６ｑ＝０

が重解を持つことから、　６４＋１６ｐｑ＝０　よって、　ｐｑ＝−４

　また、４ｑ＝ｐ² なので、　ｐ³＝−１６　より、　ｐ＝−２　で、　ｑ＝（）²

　したがって、接線の方程式は、　２（ｙ＋（）²）＝−２ｘ　より、　ｙ＝−ｘ−（）²

　この接線に関して、点（０，１）と対称な点の座標（ａ，ｂ）を求める。

　（ｂ−１）/ａ・（−）＝−１　より、　ａ＝（ｂ−１）

　（ｂ＋１）/２＝−（ａ/２）−（）²　より、　ｂ＋１＝−ａ−２（）²

　よって、　ｂ＋１＝−（）²（ｂ−１）−２（）²＝−（）²ｂ−（）²　より、　ｂ＝−１

　このとき、　ａ＝−２　で、対称点は、準線 ｙ＝−１の上にある。

　同様に、この接線に関して、点（２，０）と対称な点の座標（ａ’，ｂ’）を求める。

　ｂ’/（ａ’−２）・（−）＝−１　より、　ａ’＝ｂ’＋２

　ｂ’/２＝−（ａ’＋２）/２−（）²　より、　ｂ’＝−ａ’−２−２（）²

　よって、　ａ’＝−（）²ａ’−２（）²−４＋２＝−（）²ａ’−２（）²−２　より、

　ａ’＝−２　このとき、ｂ’＝−２（）²　で、対称点は、準線 ｘ＝−２の上にある。


（コメント）　上記で得られた結果は、２点（０，１）、（２，０）を共通接線に関して対称移動させ
　　　　　　る（これは、折り紙的には折り返すということ！）と、それら２点はそれぞれ準線上
　　　　　　に移るということである。このとき、長さを作図することが出来る。

　この２点を所要の直線上に移す操作は、定木・コンパスでは出来ない折り紙特有の操作
である。